| (1) |
f(x) を区間 [a, b] で滑らかな関数とする。
ただし,この関数値を計算するのは,非常に手間がかかる。
[a, b] 内の相異なる複数の点(標本点と呼ぶ)xi に対する関数値 yi が与えられているとき,
任意の t (a<t<b) に対する関数値 f(t) を与えられた関数値から推定することを補間と呼ぶ。
|
| (2) |
サブルーチン sample(n, x, y) で,関数表を読み込む。
関数表には,区間 [a, b] において,両端を含む n 個の等間隔な標本点 xi (i=1, …, n) に
対する関数値 yi があらかじめ与えられている。
sample(n, x, y) は,標本点の個数 n,標本点の配列 x,関数値の配列 y を格納して
主プログラムへ戻る。
|
| (3) |
補間を精度よく行う準備として,t に最も近い標本点をサブルーチン find に
よって求める。
サブルーチン find(n, x, t, near) において,n, x の意味は sample の場合と同じである。
t に最も近い標本点の番号を near に格納して戻る。
|
| (4) |
(3) で得られた near を基にして,サブルーチン arrange (n, x, t, near, idx) で
t に近いものから順に,標本点 xi と関数値 yi の対に番号を付ける。
このプログラムでは,標本点が等間隔であることを利用して,順番を付けている(図1)。
例えば,3 番目に t に近い標本点は x(idx(3)),その関数値は y(idx(3)) として
参照することができる。
これ以降の説明では簡単のため,x(idx( j)) を Xj,y (idx( j)) を Yj と表す。
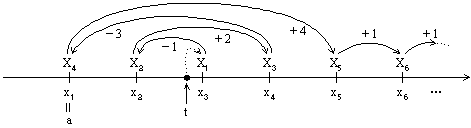
図1 arrange による標本点の番号付け
|
| (5) |
P(Xj)=Yj を満たす X の多項式 P(X) を組み立てることによって,t に
対する補間値 P(t) を求める。
k 個の標本点をすべて満たす (k−1) 次の多項式は,次のように表される。
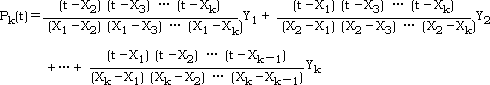
上式では標本点の組 (X1, X2, …, Xk) を用いているので,これを Pk,1(t) と表す。
標本点の組 (Xj, Xj+1, …, Xj+k−1) を用いた補間値は Pk,j(t) と表す。
|
| (6) |
k=1 のとき,(k−1) 次の多項式 P1,j(t) は定数 Yj となる。
k=2 のとき,(k−1) 次の多項式 P2,j(t) は標本点の組 (Xj, Xj+1) を用いた 1 次式となる。
同様に,k=m のとき,Pm,j(t) は標本点の組 (Xj, Xj+1, …, Xj+m−1) を
用いた (m−1) 次式となる。
これら多項式の間には,次の関係式が成り立つ。
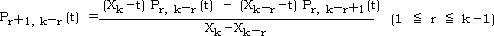
|
| (7) |
(6)の式に従い,P1,1(t) と P1,2(t) から P2,1(t) を得ることができる。
次に P1,3(t)を用いれば P2,2(t),そして P3,1(t) を得ることができる。
結局,Pk,1(t) が k 個の標本点を用いた場合の,X=t における関数値 f(t) の補間値となる
(図2)。
|
| (8) |
(7)の手続を,終了条件 EPS > | Pk,1(t) − Pk−1,1(t) |が満たされるまで,
利用する標本点の個数 k を増やしながら繰り返す。
ここで,EPS はあらかじめ与えられている小さな値である。
終了条件が満たされたときに,補間結果と利用した標本点の個数を表示してプログラムを終了する。
また,k=KMAX となっても終了条件を満たさないときには,エラーメッセージを
表示してプログラムを終了する。
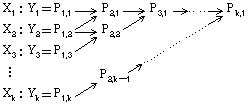
図2 反復補間法
|
program interpolate
integer, parameter :: NMAX=100, KMAX=10
real, parameter :: EPS=1.0e-5
real, dimension(NMAX) :: x, y
real, dimension(NMAX,KMAX) :: p
integer, dimension(NMAX) :: idx
integer :: i, near, k, n
real :: t, prev
call sample(n,x,y) ! 関数表の読込み
read(*,*) t
call find(n,x,t,near) ! t に最も近い点を探す
call arrange(n,x,t,near,idx) ! 標本点,関数値の順序付け
do i=1,KMAX
p(1,i)=y(idx(i))
enddo
prev=p(1,1)
do k=2,KMAX
do 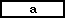 p(i+1,k-i)= (
p(i+1,k-i)= ( ) / (x(idx(k))-x(idx(k-i)))
enddo
if(abs(p(k,1)-prev) < EPS) then
write(*,'(a,f10.5,a,i3)') 'value: ', p(k,1), ', step: ', k
stop
else
prev=p(k,1)
endif
enddo
write(*,*) 'ERROR: not converged'
contains
subroutine arrange(n,x,t,near,idx)
integer :: n, near, i, j, k, m
real, dimension(:) :: x
integer, dimension(:) :: idx
idx(1)= near
if(t >= x(near)) then
i=1
else
i=-1
endif
do m=2,n
k=idx(m-1)+i
if(k <= 0) then
i=1
exit
else if(k > n) then
i=-1
exit
else
idx(m)=k
endif
i=
) / (x(idx(k))-x(idx(k-i)))
enddo
if(abs(p(k,1)-prev) < EPS) then
write(*,'(a,f10.5,a,i3)') 'value: ', p(k,1), ', step: ', k
stop
else
prev=p(k,1)
endif
enddo
write(*,*) 'ERROR: not converged'
contains
subroutine arrange(n,x,t,near,idx)
integer :: n, near, i, j, k, m
real, dimension(:) :: x
integer, dimension(:) :: idx
idx(1)= near
if(t >= x(near)) then
i=1
else
i=-1
endif
do m=2,n
k=idx(m-1)+i
if(k <= 0) then
i=1
exit
else if(k > n) then
i=-1
exit
else
idx(m)=k
endif
i= 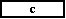 ! sign(A,B)は A の絶対値に B の符号を付けた値
enddo
do
! sign(A,B)は A の絶対値に B の符号を付けた値
enddo
do  idx(j)=idx(j-1)+i
enddo
end subroutine arrange
end program interpolate
idx(j)=idx(j-1)+i
enddo
end subroutine arrange
end program interpolate
ア (x(idx(k))-t)*p(i,k-i)+(x(idx(k-i))-t)*p(i,k-i+1)
イ (x(idx(k))-t)*p(i,k-i)-(x(idx(k-i))-t)*p(i,k-i+1)
ウ (x(k)-t)*p(i,k-i)+(x(k-i)-t)*p(i,k-i+1)
エ (x(k)-t)*p(i,k-i)-(x(k-i)-t)*p(i,k-i+1)