２次方程式の実数解の配置
＜Flash教材＞
高校数学の頻出問題である２次方程式の実数解の配置に関する問題を解くためのイメージ教材です。
この種の問題では、２次方程式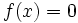 
の２つの実数解 
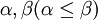と実数 
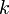の関係が
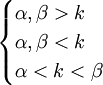
の３パターンしかないため（境界を含む場合もありますが、本質的には変わらないので省略します）、それぞれの場合にどういう条件が必要になるのかということを理解しましょう。
＜問題＞
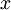についての２次方程式
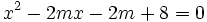
の実数解が次の条件を満たすとき、定数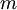 
の値の範囲を求めよ
(1) 異なる２つの負の解をもつ
(2) 異符号の解をもつ
(3) 異なる２つの実数解がともに 1 より大きい
＜解説＞
２次方程式 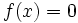の実数解の配置に関する典型的な問題です。
このような問題を解くポイントは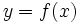 
のグラフを図示して問題を視覚的にとらえることです。
まず、２次方程式 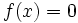の２つの実数解を 
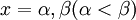とします。
すると、問題(1)～(3)の条件は次のように書き換えることができます。
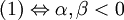
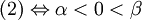
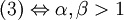
よって、(1)～(3)それぞれの場合において 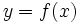のグラフを図示すると次の図１～３のようになります。
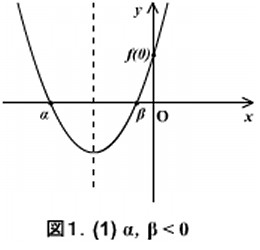
(1)の場合は、上の図１より次の３つのことが同時に成り立ちます。
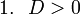
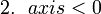
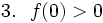
ここで注意するべきことは、２次方程式の２つの実数解と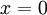 
の位置関係が図１のようになるためには、これらの３つの条件が同時に成り立たないといけないということです。例えば、上の条件(ⅰ) D > 0 と(ⅱ) 軸 < 0 の２条件のみを課すと下の図４のような解の配置も考えられるため、この場合は 
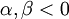とならず不適となってしまいます。
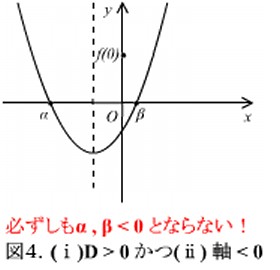
よって、この問題では上の３つの条件が同時に成り立つとして、それぞれ解いたときの共通範囲が求める解となります。
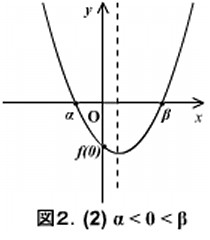
(2)も同様に考えて、実数解の配置が図２のようになるための条件は
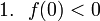
となります。したがって、この場合は上の１つの条件式を解くだけで答えが求められます。※
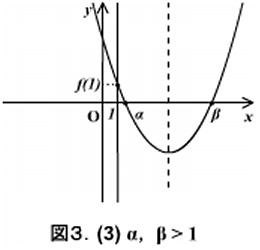
(※ 判別式 D と 軸の条件は考えなくても良いのか？と疑問に感じる方もいるかと思います。(3)の場合に成り立つ条件は、図３より次の３つとなります。
しかし、下に凸のグラフの場合、 f(0) < 0 ならば D > 0 がいえるため D > 0 の条件は必要ありません。
また、この場合の軸の位置は正負の値をとりうるので、(1)のように 軸 < 0 などと軸の条件を決めることはできません。
よって、ここで考える条件は f(0) < 0 だけで十分ということになります。)
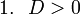
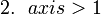
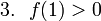
この場合も(1)と同様に、上の３つの条件が同時に成り立たないと実数解が図３の配置にならないことに注意しましょう。
＜解答＞
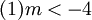
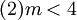
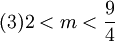
>>TOP