軌跡と方程式
<Flash教材>
軌跡とは、ある点が与えられた条件を満たしながら動いていくときにできる軌道や図形のことです。下の教材では、軌跡の中でも特に有名なアポロニウスの円 ※ をみることができます。 xy 座標上の2点 A (緑), B (青)をマウスでドラッグ&ドロップし、2点からの距離の比 m : n の値をキーボードで入力すると、その条件下での軌跡が表示されます。
※ 2点 A , B からの距離の比が m : n (m ≠ n)である点の軌跡は、線分 AB を内分する点と外分する点を直径の両端とする円になります。この円のことをアポロニウスの円といいます。ただし、 m = n のとき(2点 A , B からの距離の比が 1 : 1 のとき)の軌跡は線分 AB の垂直二等分線となります。この教材で確認してみましょう。
<問題>
2点 A (-4 , 0) , B (0 , 4) からの距離の比が 3 : 1 である点 P (x , y) の軌跡を求めよ
<解説と解答>
軌跡の問題では、まず、求める軌跡の座標(動点の座標)を (x , y) とおいて、与えられた条件を x , y の式で表します。次に、導かれた式がどのような軌跡(図形)を表すのか?という順序で考えます。
〜解答〜
問題文で与えられた条件は、
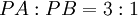
であるから、比の関係より、
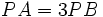
と変形できる。これを与えられた2点 A (-4 , 0) , B (0 , 4) と点 P (x , y) を用いて表すと、
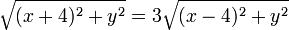
両辺を2乗すると、
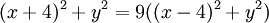
整理すると、
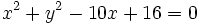
ゆえに、
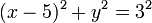
したがって、求める軌跡は中心が (5 , 0) , 半径が 3 の円
>>TOP