２次関数の最大・最小

＜Flash教材＞

２次関数の最大・最小問題に関する教材です。 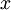座標上の点 a と点 b をそれぞれマウスでドラッグして、 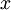の定義域を変化させてみましょう。
この教材では、 ２次関数（下に凸）における 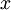の定義域を変化させたとき、最大値と最小値がどのように変化していくのかということを確認することができます。（なお、このページや教材では、簡単のため下に凸の２次関数だけを扱っています）

この教材でもわかるように、２次関数の最大・最小問題では、 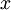の定義域の両端とグラフの軸の 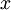座標の３つの位置関係が重要です（上の教材における 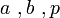）。この３つの数の大小関係によって最大値と最小値が変わっていくのですが、特に理解してほしいことは、どんな場合でも次の２点が常に成り立っているということです。

何故ならば、２次関数のグラフは軸に関して対称であり、軸からの距離が離れるほど増加していくからです。
したがって、区間内に軸があるときは、軸の位置で最小になり、軸から遠いほうの端で最大になります。また、軸が区間外にあるときは、軸に近いほうの端で最小になり、遠いほうの端で最大になります。
これさえしっかりと理解することができれば、多少複雑な２次関数の最大・最小問題でもうまく場合分けをして処理することができるでしょう。

＜問題＞

次の関数の最大値と最小値を求めよ


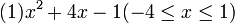
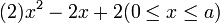
＜解説と解答＞

上の問題で、「(1)はできるけど、(2)はよくわからない」という学生が多いようです。
(2)は 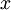の定義域に変数 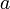が含まれ、 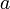の値によって 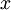の定義域が変化していくため場合分けが必要です。
２次関数 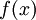の最大値と最小値を求める問題は、 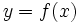のグラフを利用して解きます。
そのためにまず最初にやるべきことは、与えられた２次関数を基本形（頂点の座標がわかる形）に変形することです。

～(1)の解答～

与えられた２次関数を変形し、グラフをかいて頂点と区間の両端の値を比較して最大値と最小値を求めます。

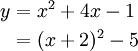
よって、頂点は 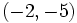になります。
また、この関数は次の２点

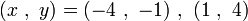
を通るので、グラフは下の図１のようになります。


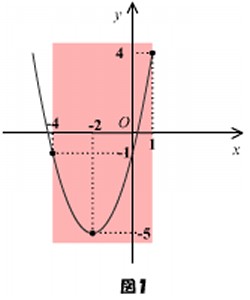
ゆえに、

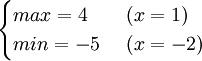
となります。

～(2)の解答～

まずは(1)と同様に、与えられた関数を基本形に変形してグラフをかきます。

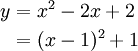
よって、頂点は 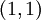になります。
また、この関数は次の点

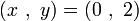
を通るので、グラフは下の図２のようになります。


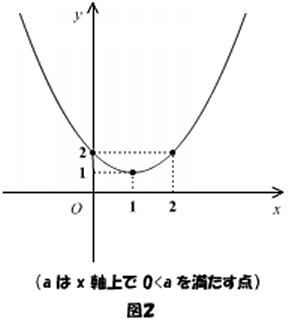
区間が 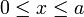であるため、 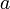が増加すると区間の右側が動いて広がっていきます。よって、下の図２-(ⅰ)～(ⅳ)のように場合分けをして最大値と最小値を求めます。



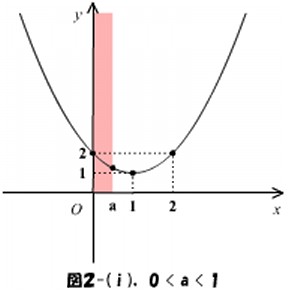
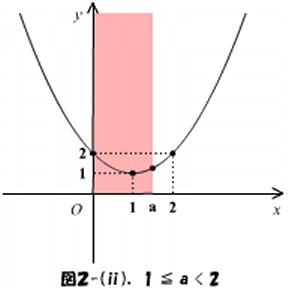
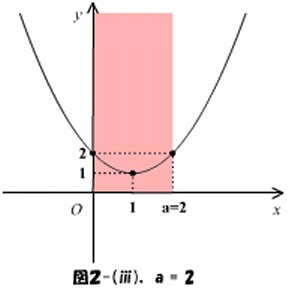
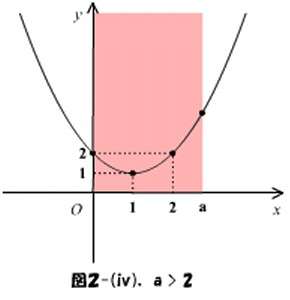
図２-(ⅰ)～(ⅳ)より、最大値と最小値は次のようになります。
(ⅰ)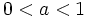

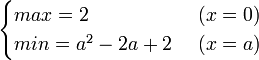
(ⅱ)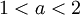

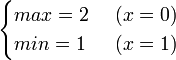
(ⅲ)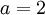

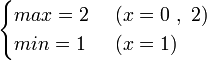
(ⅳ)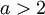

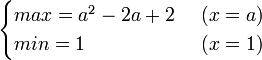
>>TOP