成分によるベクトルの演算
<Flash教材>
ベクトルの演算に関する教材です。成分によって表されたベクトルの和・実数倍の演算は次のように計算できます。
①ベクトルの和
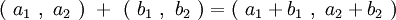
②ベクトルの実数倍
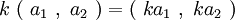
下の二つの教材を利用してこれらの計算を視覚的にみてみましょう。
〜成分によるベクトルの和〜
点 A (赤い点)、点 B をマウスでドラッグすることによって、ベクトル a , b を変化させることができます。二つのベクトルの和であるベクトル c の成分が①で示される計算上の値と xy 座標平面上における実際のベクトル c の位置が等しくなることや、下のポイントなどを確かめてみましょう。
◇ポイント◇
・ 二つのベクトルの和は、その二つのベクトルから作られる平行四辺形の対角線となる(ベクトルは平行移動しても変わらないため)
・ 成分表示におけるベクトルの和は、同じ成分どうしを足して求められる
〜成分によるベクトルの実数倍〜
上の教材と同様に、ベクトル a をマウスでドラッグすることによって変化させることができます。さらに、右下のプルダウンメニューでベクトル a を k 倍することができるので、②のようにベクトルの実数倍が計算できること、下のポイントなどを確かめてみましょう。
◇ポイント◇
・ k = -1 のときは逆ベクトルとなり、大きさは同じで向きが逆になる
・ k = 0 のときは零ベクトルとなり、大きさが 0 で向きはない(向きは考えない)
・ ベクトルを k 倍すると、大きさ(有向線分の長さ)も |k| 倍となる
<解説>
〜ベクトルの有向線分(矢印)表示〜
ベクトルとは、向きと大きさの二つによって定まる量のことです。高校数学では、よく有向線分を用いて説明されます。
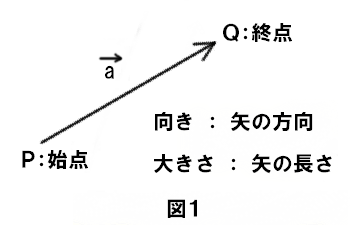
有向線分を用いることによって向き・大きさの二つを一意的に定めています。下の図でベクトル a と等しいベクトルはどれかわかりますか?
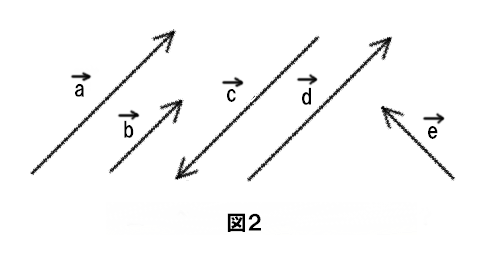
答えはベクトル d です。ベクトル a と向き・大きさの二つが等しいのはベクトル d だけで、他のベクトルは向き・大きさのどちらか一方、あるいは両方が異なっているため等しいベクトルとはいえません。ベクトル a とベクトル d は始点が異なるから等しくないと考える人もいるかもしれませんが、あくまでも問題にするのは向き・大きさの二つであって位置は関係ありません。したがって、あるベクトルを平行移動させて得られるベクトルは、もとのベクトルと等しいベクトルとなります。
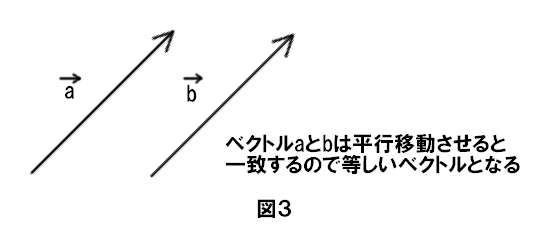
では、有向線分を書く以外にはベクトルを表す方法はないのでしょうか?
別の方法としてベクトルの成分表示があります。
〜ベクトルの成分表示〜
ベクトルの成分表示では、
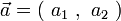
というように、xy 座標上で原点 O を始点とするベクトルの終点を示します。
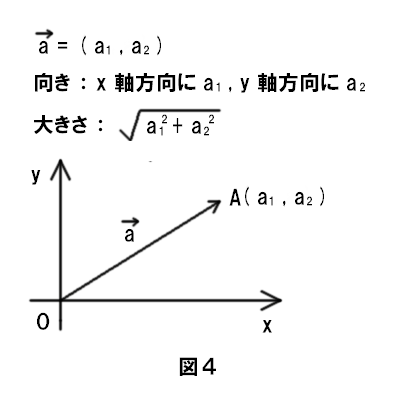
上の図4のように、ベクトルの成分表示でもベクトルの向きと大きさを一意的に定めることができます。この場合、ベクトルの向きはそのまま x , y 成分の示す方向となり、大きさは成分から三平方の定理で求められます。
>>TOP