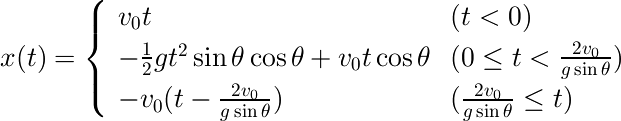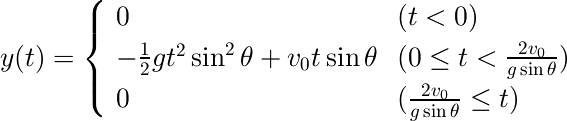大学物理入門
A guide for University Physics

様々な運動

斜方投射以外の質点や剛体の運動について、途中式を含め詳しく解説します。どんな運動も働く力さえわかってしまえば、ニュートンの運動方程式のみで解くことができます。

この教材はぜひ筆記用具を用意して、手を動かしながら、式の変形の仕方を確かめながら利用してください。

ニュートンの運動方程式: 質点の運動を記述する方程式。力学の基本として、非常に有名な式です。式はma=Fと書きますが、これは「力とは質量と加速度を掛け合わせたものである」という意味ではないことに注意してください。詳しくは「新・物理入門」（駿台文庫）を参照。

動摩擦力を伴う直進運動

なめらかではない床の上での剛体の運動を求めましょう。剛体の質量をm[kg]とし、時間0[s]における質点の位置を0[m]，速度をv₀[m/s]とします。さらに計算を簡単にする為に、質点はX軸上を運動するものとします。

物体の初速と摩擦力を示したのが次の図です。力と速度を混同して表記しており、自由物体図ではないことに注意してください。

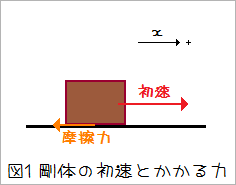
剛体と床の動摩擦係数をμとすると、X軸方向の運動方程式は

となり、これを変形して

が求められます。よってこの運動は等加速度運動であり、前提条件よりこの運動は

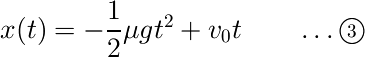
と求められます。ただし動摩擦力は物体が運動している間にしか働かないので、一度静止したら剛体には重力以外の力が働かなくなり、剛体は静止し続けます。つまり関数x(t)は、ある限定された定義域を持ちます。詳しくは後述します。

動摩擦力: 床からの動摩擦力は基本的に垂直抗力にのみ比例し、接触面積の大小や物体の速度は関係しません。垂直抗力と動摩擦力の比例定数のことを動摩擦係数と呼び、記号μで表します。動摩擦係数は剛体と床の材質，床の湿潤状態などによって変化します。

動摩擦力を伴う直進運動2

前出の問題を微積分を用いて解きなおしてみましょう。ここで、C₁およびC₂は積分定数であるものとします。

運動方程式を微分方程式の形で書き直せば、次式のようになります。

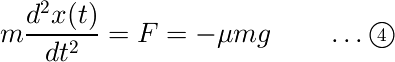
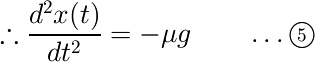
この式の両辺を時間で積分すると速度が得られます。

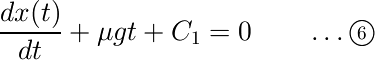
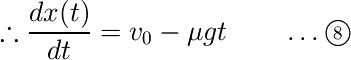
さらにもう一度両辺を時間で積分すると、位置が得られます。

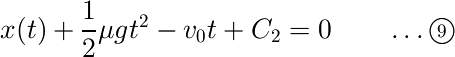
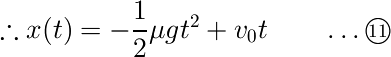
積分定数は初期条件を用いて決定します。先ほどの解き方と全く同じ解答が得られている点に注目してください。もちろん「一度静止したら剛体には重力以外の力が働かなくなり、剛体は静止し続ける」点も同じです。

斜面へ入射する質点の運動

質量m[kg]の質点が速度v₀[m/s]でX軸上正の方向に運動しています。この質点が角度θの斜面に垂直に入射したとき、この質点のx,y座標を時間t[s]の関数として求めましょう。ただし斜面に入射した時の時間を0[s]、重力加速度をg[m/s²]とします。

最高到達高度を求める

x,yを求めるのには必要ありませんが、肩慣らしにyの最大値y_max[m]を求めてみましょう。

質点には重力と斜面からの垂直抗力（この大きさをNとします）しか働いていないので、力学的エネルギーは保存されます。ですので、エネルギー保存則を用いるのが最も簡単な求め方でしょう。

斜面入射前に運動していた平面の高さを位置エネルギーの基準とすると、質点が平面上を運動しているときの力学的エネルギーE[J]は運動エネルギーK[J]だけなので、

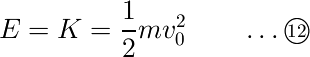
となります。

そしてこのエネルギーがすべて位置エネルギーになったときが最も高いところへ移動したときなので、エネルギー保存則よりy_maxは

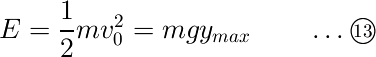
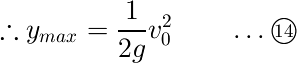
となります。

力学的エネルギー: 運動エネルギーと位置エネルギーを足し合わせたものを力学的エネルギーと呼びます。
力学的エネルギーは仕事をする・されることで変化します。今回のケースでは重力は保存力なのでエネルギーが保存され、垂直抗力は進行方向に垂直な向きの力なので仕事をしないため、エネルギーが保存されます。

x(t)を求める

それでは肩慣らしも終わったところで、x(t)を求めましょう。運動方程式を記述する必要があるので、まずは質点にかかる力の列挙から入ります。物体にかかる力は次のような自由物体図を描くとわかりやすいでしょう。見やすくする為に、この自由物体図では質点に大きさを持たせて描いています。

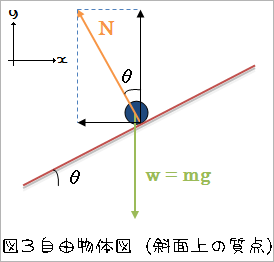
この自由物体図からも分かるように、斜面上で質点に働くX軸方向の力は垂直抗力のX方向成分のみです。よって運動方程式より

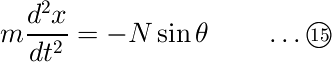
となります。しかしまだ垂直抗力の大きさNが分かっていませんので、まずはNを求めましょう。さて、Nは何を利用して求めれば良いでしょうか？

以上で垂直抗力の大きさが求まりました。これで先ほどの(15)式を解くことができます。先ほどの「動摩擦力を伴う直進運動2」と同様に初期条件から積分定数を決定すると、

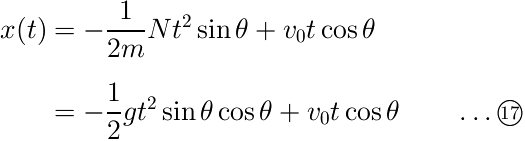
と求まります。ここで気をつけたいのが、問題文中に定義されていない変数を消去する必要があることです。垂直抗力の大きさNは独自に定義したものなので、問題文中で与えられている変数θ,m,gを用いて書き換える必要があるのです。

「力」と「力の大きさ」、「力の成分」: 大学の物理学で「力」と言えば、それはベクトルであることが普通です。「力の大きさ」ならばそのベクトルの大きさ（スカラー・負にはならない）となり、「力の成分」ならばそのベクトルの成分（スカラー）を指します。

y(t)を求める

それでは最後にy(t)を求めましょう。先程と同じように自由物体図を参考に質点にかかるY方向の力を列挙すると、重力と垂直抗力のY成分のみであることがわかります。よって運動方程式は次式のようになります。

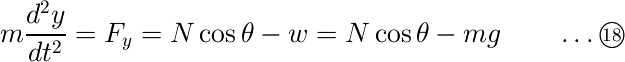
ここでY軸は上向きを正としているので、Y方向の力F_yは（垂直抗力-重力）と書く必要があることに注意してください。ベクトルを用いて表記するならば、次式のようになります。

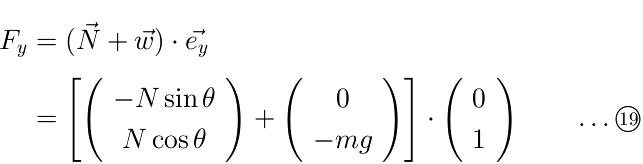
さて(18)式に(16)式を代入してNを消去し、両辺をmで割ると次式が得られます。

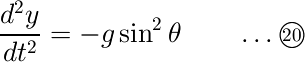
あとは初期条件を用いてこの微分方程式を解くだけです。答えは次式のようになるはずですので、計算してみてください。最大値が(14)式に等しいことも確認できると思います。

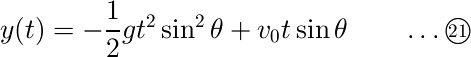
x(t),y(t)の定義域について

以上でx(t)およびy(t)が求まりました。しかしひとつ忘れてはならないことがあります。それはこれらの関数の定義域です。質点の座標がこれらの関数で求められるのは、質点が斜面上にある間だけです。よってこれらの関数はすべてのtに対して有効ではなく、ある範囲のtに対してのみ有効となります。

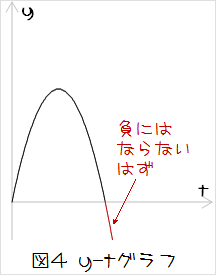
これはグラフを描けば分かりやすいでしょう。例えば(21)式をグラフに表すと次のような放物線になりますが、本来yは負にはならないはず（なぜならば平面の高さが0）であり、この式（関数）が常に正しい結果を与えてはくれないことが分かります。

それでは、どのようにして定義域を決定すれば良いのでしょうか。

以上で、定義域が求まりました。この結果から、この問題の最終的な回答は次式のようになります。

大学物理入門A guide for University Physics