概要

Javaを使い、静電ポテンシャルをガウス・ザイデル法で、境界条件を変えて解いた。
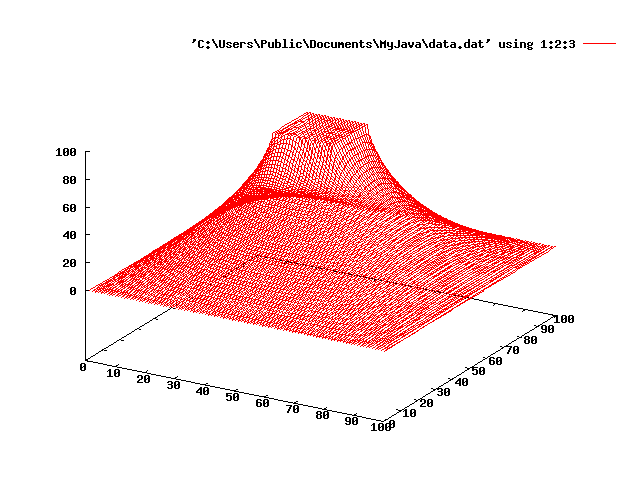
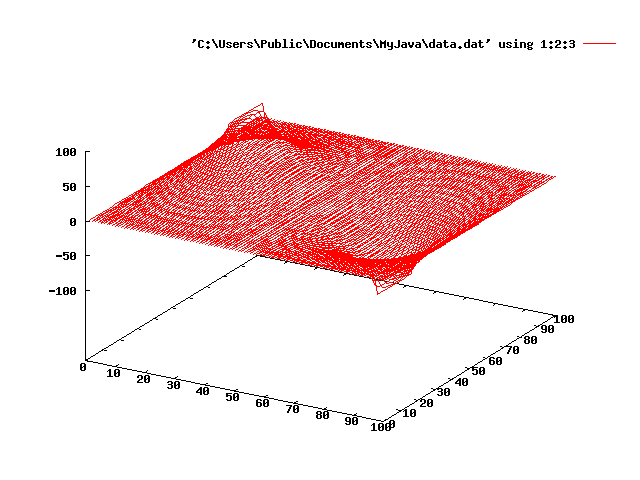
出力結果をgnuplotでグラフ化すると下のようになる。

縦と横は、接地された正方形の領域の位置を示す。
高さは静電ポテンシャルの値を示す。

ソースコードの説明

１.各変数の宣言をする。
    二次元の配列U（静電ポテンシャル)を用意する。

２．配列Uを初期化する。

３．変数kを用意して、大きい数（５０００回）、ループさせる。
     境界条件を選ぶ。
     接地部分を除く全てのiとjに対して、corrとU[i,j]の計算を行う。

　　多数回繰り返すのは、時間が大きくなるとU[i,j]が定常状態になるからである。

      corrはある点U[i,j]の周りの4つの点の平均とU[i,j]の差分であり、
      それを足したのが新しいU[i,j]となる。 それを多数回繰り返すという計算である。 

結果の説明

上から図１、図２、図３である。それぞれソースコード１、２，３に対応する。

図１：断面が正方形の周りが接地されている導管がある。その中心の導線のみに100Vの電圧をかけたときの管内の電位。
図２：接地された正方形の箱の中に、電圧がかかった箱がある場合の電位。
図３：:接地された正方形の箱の中に平行平板コンデンサーがある場合の電位。