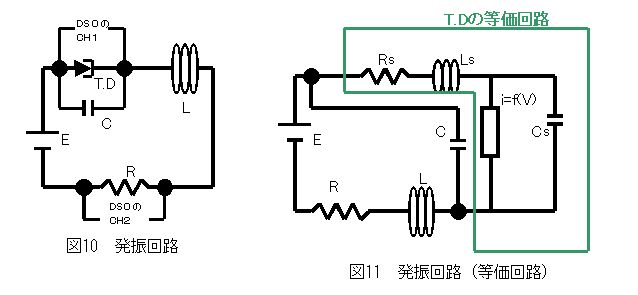
トンネルダイオードの静特性には特徴があることがわかっただろう。では、 なぜ発振回路は発振したのだろうか？静特性が大きく関わっていると考えられる。

　なぜ、発振が起こったのかわかったかな？
　次に、実験１で用いた発振回路の回路方程式を解いてみるが、 その前に等価回路という考え方を勉強しておこう。
　等価回路というのは、新しく発見された素子を、その電気的な特性をそれと等しい動作をする ように、コイル、コンデンサー、抵抗などの組み合わせであらわした回路である。トンネルダイ オードの等価回路を考えて、発振回路全体をみてみよう。

　図10の回路は実験１で用いた発振回路である。トンネルダイオードの等価回路を考えると、図10の 回路の緑色で囲まれた回路になる。図11の回路は図10の発振回路を トンネルダイオードを等価回路で置き換えて考えた回路である。

　図11の等価回路において、R_s、L_s、C_sは非常に小さいので無視 する。さらに、この運動の原理を考えると、Rも無視できる。電源電圧Eは、図12の回路のVにあたる。 そうすると最終的には図12のような回路が考えられる。

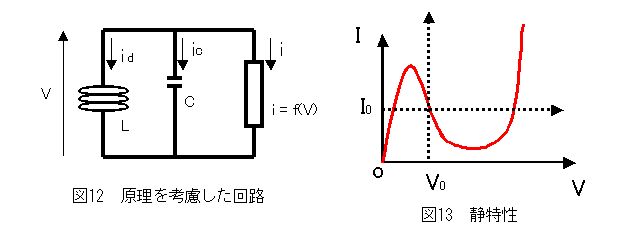
i = f (V) は、静特性をあらわす部分である。

ただし、原点を（V₀、I₀）に移動させた三次関数であらわされる。

すると　i = f (V) = - α V + β V ² + γ V ³　(α,γ>0)　とおける。

問題２．図12の回路の方程式を解いてみよう。

参考書

エンジニアリング・サイエンス講座 「非線形回路論」

〜ヒント〜
　-i_c = i_d + i
　i = f (V) = - α V + β V ² + γ V ³

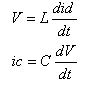
とおいて解く。
途中　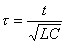　と置き換える。