1部３Ｂ「金属試料の格子比熱容量の測定」補助プリント

〔実験手順〕

1.　窒素の沸点での測定

　　START

  • 装置、机の回りを整頓しホコリ等は拭き取ること。

  • 切り換えコックを開けて全系統を真空に引け（油回転ポンプに白衣等を巻き込まれぬように）。

  • ガイスラー管で10 [Pa]になった事を確認せよ。（真空密着の項参照）。

  • 油回転ポンプは終了まで回しておく。ガイスラー管は高電圧で放射線も出すので注意せよ。

  • 冷接点冷却器に氷を詰めイオン交換水を８分目程満たせ。蓋は軽く締める。

  • KETHLEY製デジタルボルトメータ（Model 2000 Multimeter）とノートパソコンをIEEE-488(GPIB)を使ってつなぐ。（Model 2000 Multimeter裏にある）

  • 回路を点検した後、Model 2000 Multimeterをウォーミングアップせよ。電流設定ダイアルは0.06[A]とせよ。ただし、試料にはまだ通電しない（注　OUTPUTボタンOFF）。直流安定化電源のスイッチは本体の後ろにある。

  • パソコンを起動させる。（バスワードを入れずにキャンセル）

  • LABVIEWを起動させる。（デスクトップ上のnew0924a.viを開く）

  • デュワー瓶に液体窒素を８分目程満たせ。※）（保護ゴム手袋を用いて行え。）

  • 試料下方よりデュワー瓶を静かに挿入せよ。※※）

  • 試料は熱損失を最小にするため、信号線のみで吊り下げられているので、振動は絶対避けよ。付属のラボジャッキを用いるが、デュワー瓶の底がクライオスタット試料部にぶつからないように注意せよ。

  • 真空切り換えコックを、全経路遮断の中間位置にせよ。固いときは、ドライヤーで暖めよ。

  • 高圧および真空経路がすべて理解出来た上で操作に移ること。

  • 窒素ボンベは高圧、ポンプは真空で、双方とも操作を誤ると危険である。少しでも不明な点は先生に聞くこと。

  • 切り換えコックを回して、ボンベと試料室をつなげ。

  • 圧力調整器の微調弁を反時計回りの閉じた状態（緩く回る状態）にして、ボンベの元バルブを反時計回りにして開けよ（ボンベのバルブレンチは準備室）。

  • 圧力計が振れたらただちにボンベの元バルブを締め、調整器の弁により熱交換ガスとして窒素ガスを試料室に満たす。満たした後は切り換えコックを回し系を遮断せよ。圧力計（ボンベ側）が、20[kg/cm ]以下の場合は準備室に報告せよ。

  • new0924a.viの「操作」を選び「実行」を押す。（Or左上の⇒ボタンを押す）

  • 試料温度が５分間で±0.5[K]以内の変化になるまでまて。

  • 温度は、クロメル-コンスタンタン熱電対起電力表（CR-C、Ｅ型）より換算せよ。

  • ”電力入力前”基線測定

  • 切り換えコックを回して試料室の熱交換ガスを排気し、そのままで、５分間に±0.3[K]の温度変化になるまで待て。

  • 準備段階終了

  • new0924a.viの「操作」をえらび「停止」を押す。

  • カーソルをnew0924a.viのグラフ上で右クリックを押し、「データ処理」から「チャートをクリア」を選ぶ。

  • new0924a.vi 中のtotal time（測定時間）、interval（測定間隔）を設定する。（測定時間2400秒、測定間隔5秒）

    • ５分間安定したらさらに2-５分間測温し電力入力前の基線とする（計7-10分間）。

  • ”電力入力”昇温測定

  • 基線がとれたら、正確に電力を入力する。（直流電源のOUTPUTボタンON）

  • ”電力入力後”冷却曲線測定

  • 電力入力終了後、約10分間、冷却曲線を求めよ。

    • ・測定が終了したら保存ウィンドウが出てくるので、ファイル名をつけてからデスクトップ上に保存する。後でUNIX上の各自のディレクトリに保存する。

    ・UNIXに保存する場合は、FFFTPを使用する。詳しくは、学生実験のホームページhttp://www.rs.kagu.tus.ac.jp/~phlabex/LabExercise/index.htmlにある「FTPによるデータ転送の仕方」を見ること。

    ・UNIXへの保存が終了すれば、パソコンのデスクトップにある各自が作成したデータは不要になるので削除すること。バックアップが必要であれば、ネットワークに接続している実験準備室のパソコンの[学生実験]ー[実験データ]ー[格子比熱]のフォルダ内に残しておくこと。

    　ファイル名　

    　　　一　窒素の沸点での測定の場合　→　窒素＋学籍番号下3桁（窒素×××）

    　以下ファイル名は

    　　　ニ　混合液中での測定の場合　　　　　　→　混合×××

    　　　三　時間がまだ一時間以上ある場合　　　→　混合_×××

    　　　四　イオン交換水＋氷の共存温度での測定→　共存×××

    　　　五　水の沸点での測定　　　　　　　　　→　水×××

  • 冷却曲線が求まったら切り換えコックを全経路遮断の中間位置に回して、試料室を真空のまま、外系と遮断せよ。

    • 　　”上昇温度の見積り”

  • 冷却曲線を 1 or 2 Cycleの片対数グラフにプロットし、電力入力時の中点での温度を求めよ（外挿）。

  • 縦軸にはＴcool　-Ｔf（（４）式）を取る。

  • ”昇温前の基準温度”

  • 入力前の基線を入力時間の中点まで外挿し、昇温前の初期試料温度Ｔとせよ。

  • Ｔ-Ｔ０=ΔＴを昇温値とする。

  • 比熱容量を算出せよ。

    • 実験終了後必ず毎回器具の点検、整頓、水滴の拭き取りをせよ。

    本実験で用いる油回転ポンプは、電源を切ると同時に電磁リーク弁が作動するので、手動によるポンプへの大気導入は必要ない。

  • END

    • 　　2.（液体窒素+エチルアルコール）混合液中での測定

  • Start

  • デュワー瓶を静かにはずし、別のデュワー瓶に８分目程度、用意したエチルアルコール中に、残った液体窒素を静かにいれよ。

  • この混合液の場合は、温度定点とはならない。残留窒素量により190〜240[K]の間で安定した温度で測定する。

  • エチルアルコールは、８分目以上入れてはならない。

  • 実験_の※）のみ抜かして実験を進めよ。

  • 冷却曲線が直線近似できる場合は直線で補外せよ。

  • 当日の課題が終了したら、残ったアルコールを専用ポリタンクへ戻せ。

  • デュワー瓶、ポリタンク等は装置奥へ収納せよ。

    • 　　3.時間がまだ1時間以上ある場合

  • 2.の混合液にデュワー瓶の1/4〜1/5程度の液体窒素を静かに注入し、その安定温度で比熱を測定せよ。

    • 　　-参考-

  • 物理では、「比熱」という用語は未だ一般的であるが、科学系を中心として、最近、単位質量あたりの熱容量は「比熱容量」という用語に変わりつつある。

  • 本実験では、周囲温度が一定として、図５の解析をするが、電力入力前の基線がＴｂ[K]=at[min]+bの時間変化を示す場合（４）式右辺にＴｂを加えて解析せよ。

    • 　　第２週目の実験

  • 4.（イオン交換水+氷）の共存温度での測定

  • ＳＴＡＲＴ

  • デュワー瓶に破砕した氷とイオン交換水を８分目程度満たせ。

  • 実験_の、※）のみ抜かして実験を進めよ。

    • 　　5.水の沸点での測定

  • ＳＴＡＲＴ　

  • 沸点測定器に水を８分目程度（水タンクの）満たし、ヒーターと共にクライオスタットに静かにセットせよ。

  • ヒーターをONにし、沸騰するまで待て。

  • 水圧計Ｍの、水柱の高さｈをノギスで読みとれ。空だきに注意。

  • 実験_の※）、※※）を抜かして実験を進めよ。

  • 冷却曲線の測定後は、常に切り換えコックを全経路遮断の中間位置に回して、資料室　を真空に保ったまま外系と遮断せよ。

  • すべての実験終了後、器具の洗浄、整頓をし、トラブルのある場合、準備室に報告せよ（デュワー瓶、ポリタンク等は装置奥へ収納せよ）。

  • 実験値をＣに変換し、デバイの理論曲線と比較せよ。

    • 　　-水の沸点の求め方（図４参照）-

    気圧がＨ[Torr]とすると沸騰水の表面に加わる圧力Ｐは、

    Ｐ＝Ｈ+　　[Torr]　　（１）

    である。ｈ[mm]が一定になったときの圧力Ｐに対する水の沸点Ｔは、373[K]、　　　　760[Torr]付近において、

    Ｔ=373.15[K]+0.0367(P-760)[K] (2)

    で与えられる。

    （ただし、第二項の補正は、有効数字をよく考慮して採否を決定せよ）。

    -定圧比熱Ｃと、定積比熱Ｃとの関係式-

    Ｃｐ＝Ｃｖ（1+γαＴ）　　　　　　　　　　　（３）

    ここでγはグリューナイゼン定数、αは定積膨張係数を表す。アルミニウムの場合は　γ=2.17、α=6.9×10　[K ]である。

    -試料の温度上昇ΔＴ＝Ｔ-Ｔ０の求め方-

    恒温壁法における熱交換の補正は、加熱前後における試料温度の時間変化を追跡して、グラフまたは計算から求める。この時間変化はニュートンの冷却の法則にしたがうと考えられるので、

    T-Tf =A exp[-α’t] (4)

    の曲線になるはずである。

    ここでＴfはｔ→∞としたときの終局温度とする。その決定には、

    ｔ3= (ｔ1+ｔ2)　　　　　　　　　（５）

    の関係を持った時間ｔ1、ｔ2、ｔ3　のそれぞれの温度Ｔ、Ｔ、Ｔ　において、

    　　　　　　　　　　　　　　　　　　　　（６）

    の関係を用いる（証明は（４）、（5）より容易にできる）。また（4）においてｔ=0とすれば、

    A=TI ―TF

    Ｔは供給電力を切ったときの温度とする。そして、

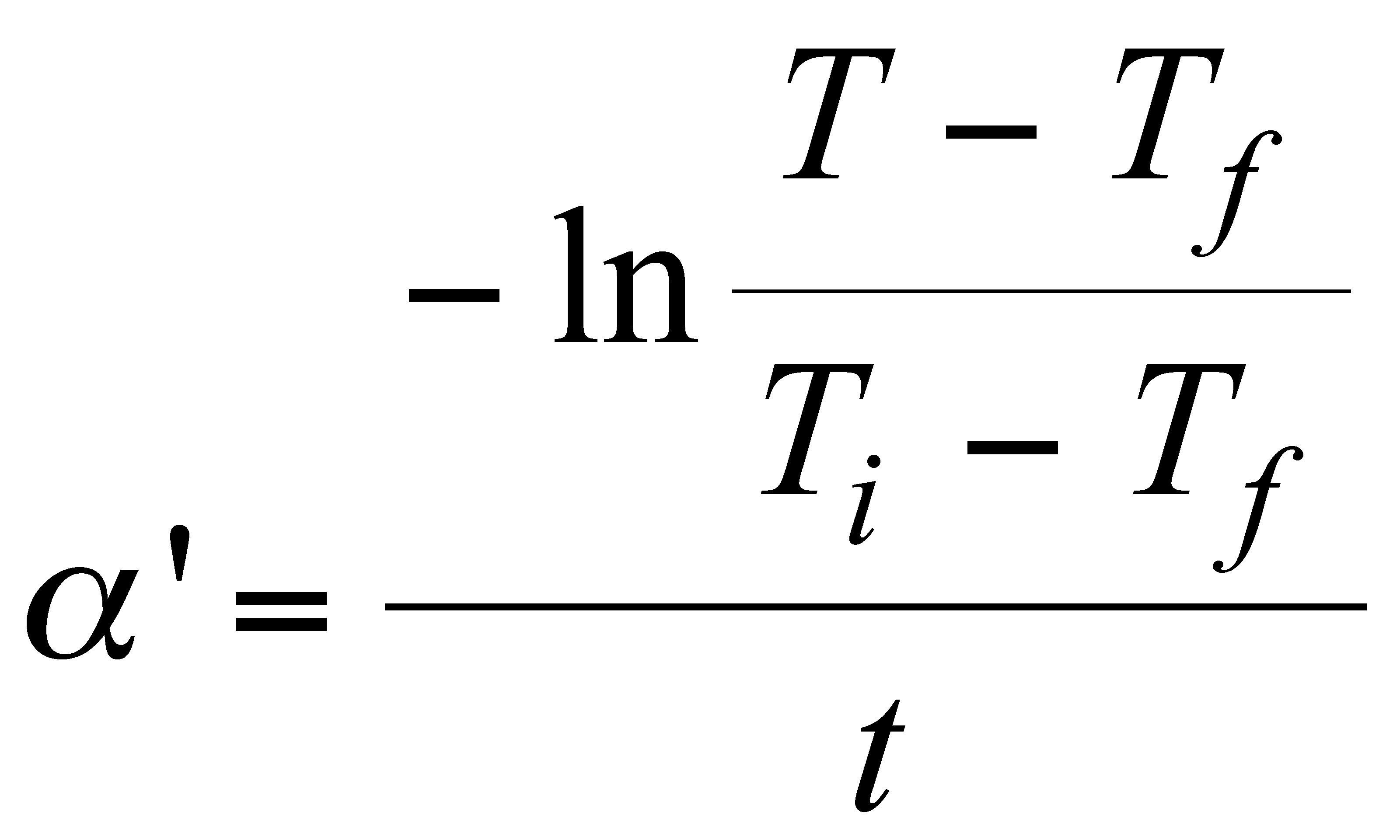    　　　　　　　　　　　　　　　　　　　　（7）

    よって加熱前後の温度変化が見かけ上、一定速度で起こるものとすれば、これらを加熱期間の中点に補外して、試料の初期温度Ｔおよび上昇温度Ｔを求める。この時、ｔ、ｔ、ｔは、何通りか選択して計算。考察し、最も妥当なＴ、Ｔを求める。

    すると、試料の定圧比熱は、１モルあたり

    　　　　　　　　　　　　　　　　　　　　　　　　　（8）

    で求められる。ここでＶ、Ｉ、ｔは、試料ヒーターに供給する電圧[V]、電流[A]、時間[sec]、を表し、ｍはモル数を表す。ここで Alの原子量は26.98154[g]、１[cal/mol]=4.1840[J・mol-1]4.1840[J・mol-１]である。

    　

    [考察]

    これは、一人一人が本実験を通じて熟考した物理的内容、結果の妥当性等を論ずるもので、ユメユメ参考文献の書き移し等であってはならない。

    TEXT中の問、付表、式等は考察の一助として用意したので、必ずすべてに目を通し解答せよ。

    問1.（3）式のＣｐ-Ｃｖの関係を、熱力学的方法から導け。ただし、γはグリューナイゼンの関係式、

    で表され、αは体膨張係数、Ｖは体積、χは圧縮率である。

    問2.　デュロン・プティの法則、アインシュタインの比熱理論、デバイの比熱理論の相違　　　を述べよ。

    デバイ温度と格子の振動数の関係を具体的に述べよ。

    金属の比熱には、格子比熱の他に電子比熱の寄与もあるという。双方の間の関係および温度領域の範囲を説明せよ。

    測定点を滑らかな線で結び、そのＣの値をもとにして液体窒素雰囲気より、水の沸点雰囲気での測定の間の、エントロピー変化

    を求めよ。それを縦軸にエントロピー、横軸に絶対温度をとってグラフで示せ。

    10[K]毎に計算すると、例えば窒素温度からだと

    から、８２Ｋでのエントロピー平均変化量ΔＳ８２ [J/K]が求まる。以下、水の沸点まで同様にして計算できる。

    なぜ、一般に理論ではＣＶ、実験ではＣＰが用いられるのであろうか、課題2と合わせて考えてみよ。（ＣＰについてのヒント：実験で直接Ｃを求めることができるだろうか？”金属の熱膨張”の解説も読んで見よ。

    　

    ｛参考文献｝

    “固体物性”の本ならば、いずれも可。

    　

    謝辞：本実験の情報処理教育の導入に当たり、元大学院生高沢章博士、水野統太氏、理数教育卒業研究生山本岳氏のご協力を得た。茲に厚く謝意を表す｡