- まず放射線の人体に与える障害である。しかしながらこれから取り扱う放射線は非常にわずかであるから恐れる必要はない。かといって油断して不用意に放射線の照射を受けると場合によっては障害を生ずるかも知れない。したがってできるかぎり放射線の被曝を少なくするように実験の方法など考えるべきである。ここで取り扱う放射線源は密封された線源であるから放射性物質が体内に入るおそれはほとんどない。しかし念のため実験中はなるべく手袋を使用して皮膚などが線源に直接触れないように心がけてほしい。実験後、放射線源は所定の位置にもどすことが大切で、そのまま放置して後から実験する人に過大な照射を与えないようにしなければならない。実験中、放射性物質を破損などした場合はただちに申し出て指示を受けることを必ず行ってもらいたい。
- ここで取り扱う放射線測定器は簡単なように見えるが、一般の電気計測器に比較して桁違いに高い感度をもっている。電流測定に例をとってみると、一般の電流計測では現在のところ最高の感度は 10-15 [A] 程度である。一方一見構造が非常に簡単な GM 計数管においてすら電子を一個一個検出できる能力を持っている。仮に毎秒一個の電子を検出したとすれば電流に換算して 10-19 [A] となる。したがって取り扱いには十分注意して慎重であることが大切である。そうでないと得られたデータの信頼性が小さくなるのみでなく、測定器を破損するおそれもある。
(3) 上述の注意に加えて、これから述べる諸注意をよく守り、実験の目的、機器の動作原理、操作をよく理解して誤りのないよう実験が行われることを希望する。
- 実験はこれから説明する「GM 計数管の特性」・「β線エネルギーの測定」の2種類を行う。おのおのの実験はだいたい6時間程度で終了するように組み立てられているが測定器の作動操作などについてはあらかじめ熟知していないと時間内に実験が終了しない場合がある。予習を十分にして、放射線計測の基礎技術を習得することをのぞむ。
(1) GM 計数管の動作原理
GM 計数管は放射線による気体の電離作用を利用して放射線の強さを測定する装置で、電離作用によってひき起こされた“電子なだれ”による電圧パルスの数を計数するものである。たとえば図1のような構造(端窓型 GM 計数管の例)の管にアルゴン(100 [torr]) とエチル・アルコール(10 [torr])ガスを封入した GM 計数管に、電離を起こさせるような粒子が入射すると、その道すじにそってイオンを作り、電子は心線に向かってすみやかに移動する。心線付近は電界がより強いため、荷電粒子は加速され中性分子に衝突、イオン化する。ここではこの現象が特にひんぱんに起こり、いわゆる“電子なだれ効果”により心線に大きな電流脈流が生ずる。この電流が抵抗を通って流れるとき抵抗の両端に電圧脈流が生じてこれを電子回路で増幅して計数する。
電子なだれのため外周円筒(陰極)には陽イオンが流入する。陽イオン (Ar+) は移動中にアルコール分子と衝突してその電荷をアルコール分子に移す。アルコール分子だけが陰極に到達し中和される。その結果、生ずる励起エネルギーは放射されたり無放射遷移によって金属電子に移ったりする代わりにアルコール分子が解離する。このような型の GM 計数管を自己消滅型と称し、市販されている GM 計数管のほとんどはこの型に属する。GM 計数管では放射線による一次電離の数に無関係に一定の大きさの出力電圧が出るような印加電圧で動作させる。
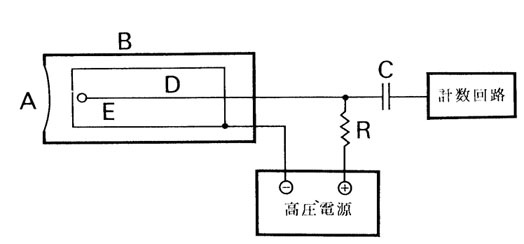
図1 GM 計数管の構造
A : 薄窓 (Mica or Al) B : ガラス円筒 D : 金属円筒 E : タングステン線(陽極)
(2) プラトー
GM 計数管はさきに述べたような単純な構造のため製作も容易であるが、原理からいって放射線による電離が一種の引き金になって電圧パルスを発生させるため、放射線の種類を区別することはできず電離を引き起こすものは無差別にすべて計数する。GM 計数管に印加する電圧を変えて一定条件の放射線を計測すると図2に示すような関係が得られる。Vsを始動電圧、Va〜 Vb間を GM 計測管のプラトーと呼ぶ。この部分では計数が印加電圧の変化に依存することが少なく計数につごうがよい。放射線を測定する場合はプラトーの長さの Va より 1/3 のところを動作電圧 (Vo) とする。プラトーにはわずかの傾斜があり、100 [V] あたりの計数の増加する割合をプラトーの傾斜といい (ΔC/C×100)÷100 [V] (C:カウント数)で表す。GM 計数管の良否を判定する一つの目安になる。
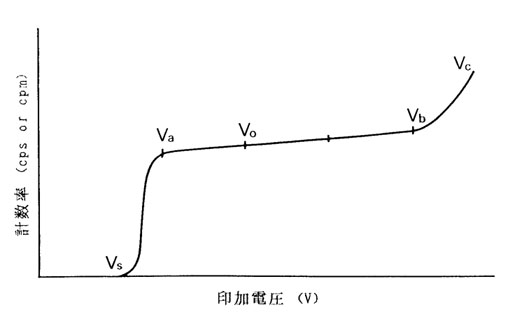
図2 GM 計数管の電圧特性
(3) 偽計数・不感時間・分解時間・回復時間
プラトーには若干の傾斜がついている。これは印加電圧を上げると GM 計数管の有効領域がわずかずつ増加するため、およびアルコール分子の分解により放電の消滅が完全に行われなくなるためである。後者によって計数が増大する場合を偽計数と呼んでいる。このほか偽計数には GM 計数管の電極間の絶縁不良や計数回路の不良によるものがある。
強い放射線源の近くにおいた GM 計数管の出力を増幅してオシロスコープに接続すると図3に示すような波形が観測される。右側に並んでいるのは、左側のパルスが生じた後、計数管内にはいった放射線によってひき起こされたパルスである。図に見られるように最初のパルスが生じてから Td 以内にはパルスが現れず、また T 以内ではたとえパルスが現れてもその高さが低いので計数されない。そして Tr に至って初めて元と同じ高さのパルスが生ずる。Td、T、Tr をそれぞれ不感時間、分解時間、回復時間という。Tの大きさは GM 計数管の大きさによって変わるがだいたい 10-4 [sec] ぐらいであるから計数が大きくなると数え落しをするようになる。
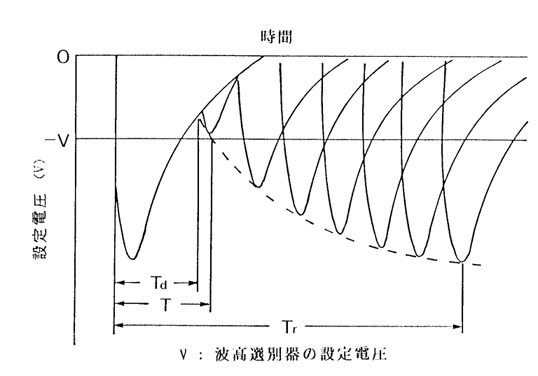
図3 GM 計数管の出力波形
(4) 二線源法による分解時間の測定
GM 計数管によって放射線の強さを測定する場合、その測定し得る計数率の限界は GM 計数管自体の分解時間によって決まる。これはその封入ガスの種類、その圧力および計数管の寸法によって変わるが、同一計数管でもこの分解時間は計数管の印加電圧の変化にともないその値が変わる。実際に問題となるのは計数装置を一緒にした場合の分解時間である。
いま計数管に入射する電離性粒子が毎秒 N 個とし、実際、計数装置で読み取られる計数率は毎秒 n 個 (N > n) であるとすると、1秒間の分解時間の総量は nT 秒となるから、1秒間の計数損失は
となり、計数損失の割合は n に比例する。この式(a)を変形して
近似的に
2個の放射線源をとり、それぞれ単独に測定した場合の計数率をおのおの n1、n2 とし、両者を合わせて同時に測定した場合の計数率を n12 とする。実際に計数管に入るこれらの値を N1、N2 および N12 とし自然計数率の値を nb とすれば、
N1 = n1 + n12T - nb (d)
N2 = n2 + n22T - nb (e)
N12 = n12 + n122T - nb (f)
式(c) より 式(d) + 式(e) = 式(f) であるから
∴ T =( n1 + n2 - n12 - nb )/( n122 - n12 - n22) (g)
ここで測定値の統計的誤差は無視してある。実際には計数値を大きくして測定を行う。また、自然計数率の値は小さいので、この計数損失は無視しうる。
(5) 計数の統計
原子核の崩壊は確率的な現象であるから、計数率毎分 r の一定の放射線源を計数する場合 t 分間の計数値はつねに r t になるとは限らず、r t の付近に分散した値が得られる。今、測定回数を n、各回の読み xi とすれば、この平均値
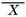 は
は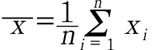
となる。これらの測定において各回の読みの値は平均値に対してばらつく。この分散がポアソン分布で与えられるとすれば平均値からの標準偏差は
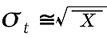 (h)
(h)で表せ、多数回の測定を行ったとき、測定値の約68%がこの偏差の中におさまる。 一方、真値 r からの標準偏差は
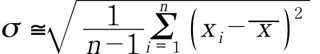 (i)
(i)で表わせる。もしが忠実に r を表わす(すなわち、測定が十分正しく行われている)とすれば、式(h)と式(i)はほとんど等しいはずであり、両者を比べることは測定の信頼度のチェックとして役に立つ。σ が σt よりかなり大きいときは、この測定器には各回の値をばらつかせる原因として統計的動揺以外の原因があることを意味する。その原因としては、たとえば計数管の偽計数の増大、付近にある放射線源の変化などがある。
(6) GM 計数装置の構成
GM 計数管により生ずる電圧パルスを数えるには図4のような 電子回路を用いる。電圧パルスの大きさは普通の GM 計数管では 0.1〜10 [V] に達するので増幅は簡単である。波高選別器は外部からの雑音などを拾わないためのもので、ある電圧レベル以上のパルスによってのみ作動し、後段に一定のパルスを送る。計数回路の基本回路は2進法で、このような回路を適当に組み合わせて 10 進法の回路としてあるのが普通である。
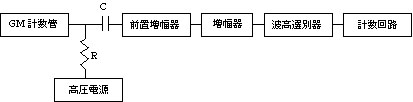
図4 計数装置の回路構成
(7) 使用放射線源について
- 90Sr - 90Y : GM 計数管のプラトー曲線の測定に使用する。
- 204Tl : β線の吸収曲線の測定に使用する。
- 90Sr - 90Y : 二線源法による GM 計数装置の分解時間の測定、および吸収曲線 の測定に使用する。
- 60Co :β線の 吸収曲線の測定に使用する。
A, B, D は直径 25[mm]、高さ 6 [mm] のアクリルのディスクの中央の穴に埋め込まれ、きわめて薄いアルミ膜でおおってある。
C は直径 25 [mm]のアクリルの半円板4個からなり、そのうち2個に線源を埋め込んであり、他の2個はふたの役目をする。
(8) 使用器具
- 端窓型 GM 計数管( GM プローブに固定)
- GM プローブ(鉛シールド測定台に固定)
- 鉛シールド測定台(机の上に固定)
- スケーラ(タイマー内蔵)
- オシロスコープ(貸出)
- 吸収板セット(貸出)
- 放射線源(金庫内)
- 部屋の鍵、BNC-BNC ケーブル、ピンセット、手袋(貸出)
課題1.GM 計数装置の動作の確認と波形の観察
- スケーラの電源コード、GM 計数管へのケーブルが正しく確実に接続されているかどうかを点検する。
- スケーラの OUTPUT 端子とオシロスコープの INPUT 端子を BNC-BNC ケーブルで接続する。
- 高電圧調整用つまみ(HV ADJ.)が最低の位置にあることを確かめる。
- 以上の事項を確認したのち、スケーラとオシロスコープの電源スイッチを入れ、少なくとも 30 秒間以上電気回路の " Warming up " を行う。
- 計数管の窓の下(測定台の一番下の棚)にプラトー曲線測定用線源 (90Sr - 90Y) をアルミ膜面を上にして置く。
- [PRESET TIME] を10分にセットしてから、[RESET COUNT] ボタンを押す。
- つぎに高電圧調整用つまみをゆっくり高電圧側に回していく。モニタ(スピーカ)から音が聞こえはじめたら、これが GM 計数管の始動であって、このときの電圧が始動電圧(900〜1000 [V] )である。(スピーカの音と計数指示の動作はしばしば一致しないことがあり、ふつうスピーカの音が先に聞こえ始める)。このとき波形はどのように変化するか観察せよ。
- さらに高電圧用つまみをゆっくり回し、計数管の指定使用電圧(1100[V] 位)まで印加電圧をあげる。この状態において、計数管の下の放射線源を取り去った場合、この操作に対応して計数が減少すれば、一応 GM 計数管は作動状態に入ったことになる。
- 計数装置を止める場合にはまず高電圧用つまみを最低の位置にし高電圧指示の電圧計が 0 [V] を指示していることを確かめてから電源スイッチを切る。高圧を下げずにただちに電源を切ってはならない。
課題2.GM 計数管の電圧−計数率特性(プラトー曲線)の測定
プラトー曲線から始動電圧、ガイガー開始電圧、プラトーの電圧幅、プラトーの勾配を求める方法を習得する。
- 90Sr - 90Y(プラトー曲線測定用)を線源として、始動電圧付近から 50 [V] ずつ印加電圧を上げてゆき、おのおのの電圧において1分間計数し、計数率(cpm : count per minites)を求める。
プラトーの上限電圧 Vb の付近で計数率を測定するときはきわめて慎重に注意深く行わなければならない。Vc(図2)より少しでも電圧を上げると計数管はただちに連続放電に移行し、有機ガス封入の GM 管ではその後の動作が不安定になり、使用不能になる。計数管への電圧のかけすぎは絶対に行わないよう注意しなければならない。最高電圧として 1300 [V] を目安とする。
- 横軸に計数管電圧 [V]、縦軸に計数率 (cpm) をとり、方眼紙にプロットする。
- 次に 50 [V] ずつ印加電圧を下げてゆき、おのおのの電圧において1分間計数する。この操作を2往復繰り返し、4個のデータを平均し計数率を求め、方眼紙に記入し曲線を描く。
- これより始動電圧 Vs、開始電圧 Va、プラトー長さ、動作電圧を決めよ。つぎにプラトーの長さの中央付近で 100 [V] の電圧幅に対する計数率の増加率をとりプラトー勾配 (%/100 V) を計算せよ。これは相対的勾配といわれるものである。
課題3. 計数の統計と誤差の評価
- SCALERの後ろのOUTPUTをPHS に切り換える。
- BNCケーブルの接続。SCALER OUTPUT - COUNTER INPUTA
- COUNTERの電源。
- SCALERの電源ON。プラトー用線源を入れる。
- COUNTERのCHECKを押す。→ 赤ランプが消える。
- COUNTER GATEが点滅するようにLEVELを調節する。
→ 約100Hz の値を指定周波数に応じて次々と表示する。
- PCの電源ON。(以下PC)
- OK → LabVIEW起動。
- OK OK → M-main1.viが起動。
- 時間間隔0.1sで1000 回測定する。
(1)設定 測定ファンクション 周波数
時間間隔 0.1s
測定回数 1000
(2)測定開始 左上の?を押す。
(3)測定が終了したら、データを保存する。
新規
ファイル名入力
ファイル
(4)グラフクリア
アップルキーを押しながら、グラフ内でクリックし、データ処理
より、チャートクリアを選択する。
- 時間間隔1sで1000回測定する。
- SCALERの後ろのOUTPUTをAMPに切り換える。
- データ処理は以下を参照のこと
- 平均、標準偏差を求めなさい。
- 度数分布、ポアソン分布、正規分布をグラフに表し、比較しなさい。
- GM管の良否を判定しなさい。
- 時間間隔0.1sと、1sのデータがそれぞれ得られ、保存されていることを確認すること。
- データは、「書類」フォルダの中に、各自でフォルダを作成し、その中に納めること。各自のフォルダを作らず、データが放置されている時は消去することもある。
- また、「M-main1.vi」はもう使わないので、終了させてよい。
- デスクトップ上にある「放射線計測データ変換」をダブルクリックして起動する。
- 起動するとウインドウが現れるので、変換したいデータのファイルをドラッグ&ドロップする。(ドラッグ&ドロップとは、ファイルを選択しマウスでクリックしたまま移動させ(移動中はマウスを押したまま)、目的の場所まで持ってきたら、マウスのボタンを離す動作。)
- 変換ボタンを押す。元のファイルと同じ階層に新しいファイルが作られる。変換された新しいファイルには「_」が付く。
- 得られた変換データの横軸は放射線の計数値、縦軸は度数で、これはいわゆる度数分布である。
- 変換が終わったら「file」から「Quit」を選んで、終了する。
- 変換データを、デスクトップ上にある「Kaleida Graph」にドラッグ&ドロップする。
- 「テキストファイルの入力形式」というダイアログが出る。(「タイトル読込み」オプションのチェックが外れている時は、チェックすること。)「OK」を押すと、表が出てくる。これでデータが読み込めたことになる。
- これをグラフにするには、「ギャラリー」→「線形」→「折れ線グラフ」を選ぶ。
- 出てきたダイアログで、Xを「計数値」に、Yを「度数」にする。これで、計数値が横軸、度数が縦軸のグラフができる。
- 分布の平均値を求める。計数値をx、度数をP(x)で表わすと、分布の平均は、
= Σx P(x) / ΣP(x)
である。和は、xについて取る。これを求める方法の一つを紹介する。
- ます、各xについて、x P(x)を求める。
- 「データ」→「列の追加」を選んで、表にC列を追加する。(ちなみに計数値はA列、度数はB列である。)
- 「ウインドウ」→「数式入力」を選択する。数式入力ウインドウ内に、計算式を入力する。今の場合、A列がc0、B列がc1、C列がc2、になっているはずなので、
c2=c0*c1
と入力すればよい。数式は、いくつか登録できるようになっていて、F1からF8のボタンを押すことによって、登録されたものが選べるようになっている。
「実行」を押すと、C列(c2)に計算結果があらわれる。
- Σx P(x)を求めるには、表を選択した状態で、「機能」→「統計ノ」を選ぶと、いろいろな計算結果が出てくる。ここで知りたいのは、「合計」である。
- 同様にしてΣP(x)もこの機能を利用して求めることもできるが、測定回数が1000であることからΣP(x)も1000であり、わざわざ調べるまでもないだろう。
- 以上から分布の平均値が計算できたはずである。
- ます、各xについて、x P(x)を求める。
- まず、「データ」→「列の追加」を使って、表にD列を追加しておく。ここにポアッソン分布の計算結果を収納する。
- 計算は「Kaleida Graph」ではなく、「Excel」を使う。デスクトップ上の「ポアッソン分布の計算」を開く。
- 出てきたダイアログは「OK」
- D2またはE2のセルに、求めた平均値を入力する。すでに数値が書かれていると思うが、これは消してしまってよい。
- 入力後、enterを押すと、B列またはC列にポアッソン分布が表示される。D2に入力した時はB列に、E2に入力した時はC列に表示される。計算式は、計数値をx、平均値を
とすると、次の形である。
^x * exp( - ) / x!
- Excelの表には計数値1〜200までの分布が計算できるようになっているが、実験データの方は、限られた計数値(例えば、0.1sなら計数値20強まで)しかないはずである。その実験データの計数値範囲と同範囲を「Excel」の表からコピーして(「編集」→「コピー」)、「Kaleida Graph」の表に(追加したD列に)ペーストする。(「編集」→「ペースト」) 範囲をそろえないと、グラフにする時に横軸がずれてしまうので、これには注意すること。
- D列の名前を変えておく。表の「D」とかかれた部分をダブルクリックすると、「列の形式」というダイアログが現れて、名前が変えられるようになる。
- Excelの表には計数値1〜200までの分布が計算できるようになっているが、実験データの方は、限られた計数値(例えば、0.1sなら計数値20強まで)しかないはずである。その実験データの計数値範囲と同範囲を「Excel」の表からコピーして(「編集」→「コピー」)、「Kaleida Graph」の表に(追加したD列に)ペーストする。(「編集」→「ペースト」) 範囲をそろえないと、グラフにする時に横軸がずれてしまうので、これには注意すること。
- 今度は、「kaleida Graph」で計算できる。先ほどと同様に、表にE列を追加しておく。この列はc4に対応する。(E列に4と表示されていない時は、「計数値」の所をクリックすると、「計数値」がc0に、E列がc4になる。)
- 「ウインドウ」→「数式入力」を選択する。数式入力ウインドウ内に、ガウス分布の計算式を入力する。例えば、平均値が94.0ならば、
c4=1/sqrt(2*pi*94.0)*exp(-(c0-94.0)^2/2/94.0)
となる。数式入力ウインドウに登録されていれば、それを利用できる。
- 「実行」を押すと、E列にガウス分布が表示される。先ほどと同様に、列の名前を変えておくとよい。
- 実験結果の度数分布とポアッソン分布、ガウス分布を重ねて表示する方法を紹介する。
- 表を選択した状態で、「ギャラリー」→「線形」→「ダブルY」を選ぶ。ダブルYは、横軸を左右別々に使うことのできるグラフである。
- 「計数値」をX、「度数」をY1、D列、E列をY2にする。x P(x)を計算したC列は表示しないので、そのままにしておき、「新規プロット」。
- 縦軸をそろえる。度数の方は、合計1000で規格化されているの対し、ポアッソン分布、ガウス分布は和(積分)が1になるように規格化されている。従って、度数分布の縦軸が、ポアッソン分布、ガウス分布の縦軸に比べて1000倍大きい時に両者を比較することができるようになる。そのためには、左右縦軸の範囲を比較できるように揃えなくてはならない。
- 縦軸の範囲を変えるには、軸を選んでダブルクリックする。「軸の設定」ダイアログが現れるので、最大値と最小値を入力する。例えば、度数を最大値150、最小値0としたら、分布の方は最大値0.15、最小値0とすればよい。
- グラフは、ある程度編集できる。例えば凡例記号の部分をダブルクリックすると、プロットスタイルを変更できる。また軸のラベルを変更するには、そこをダブルクリックすればよい。
- 印刷をするには、「ファイル」→「グラフィックのプリントノ」を選ぶ。「用紙設定」ダイアログが出たら「OK」。(用紙方向を横にしてもよい。)プリンタのダイアログが出たら「プリント」を押す。プリンタはこの実験室出口の廊下にある。
データ処理
データの保存場所
データの変換 <測定データを度数分布に変換>
データの読み込みとグラフ化
平均値の計算
ポアッソン分布の計算
ガウス分布の計算
グラフを重ねて表示する
以上の操作を0.1sと1sの実験データに対して行う。
計数の小さい0.1sの結果に対しては、ポアソン分布の方が近い形になるだろう。また、計数の大きい1sの結果に対しては、ガウス分布の方が近い形になるのではないかと思われる。各分布についての解説は、貸し出し器具と一緒に入っている「KNOLL 放射線計測ハンドブック 第4章」を参照するとよい。
終了について
「Kaleida Graph」を終了する際に、「変更の保存」ダイアログが出てくるが、これは「なし」を選んで終了すること。課題4. 二線源法による分解時間の測定
強さのだいたい等しい2つの放射線源を同時に用いて測定した計数率が個々の線源を別々に測ったときの計数率の和よりわずかに小さいことを実験的に確かめ、近似式より分解時間を求める。
- 計数管を動作状態にしたのち、計数管使用電圧 Vo に固定する。
- 測定台の試料棚に 90Sr - 90Y を入れて cpm で 10 回測定しn12 [cpm] を求める。
- 試料棚から線源(C2)を取り出してふたを入れ、線源(C1)を 10 回測定し、n1 [cpm] を求める。同様にして(C1)を取り出し、(C2)を入れて n2 [cpm] を求める。
- 線源を取り除きふたを2つ入れ、自然計数率を 10 回測定して、nb [cpm] を求める。
- n1、n2、n12、nb の値から式 (g) より Vo における分解時間 T [sec] を求める。
- オシロスコープによる波形の観察より分解時間を求め、二線源法により求めた分解時間と比較せよ。
一例としては
(1) ラジオアイソトープ 講義と実習
日本アイソトープ協会編 丸善株式会社
(2) プライス 放射線計測
西野 治、関口 晃訳 コロナ社
(3) ノル 放射線計測ハンドブック
木村逸郎、阪井英次訳 日刊工業新聞社